
Geodetiche
Realizzeremo alcuni semplici esperimenti utilizzando oggetti facilmente reperibili in ogni casa (un pallone, un tubo di cartone, una ciambella per bambini, una sfera di polistirolo, una bottiglia di plastica, ecc.) e materiali poveri (cartoncino, elastici, colla, spilli). Sono esperimenti che ci consentono di intuire nozioni profonde, spesso molto difficili da abbordare sul piano del formalismo matematico. Chiunque si avvicini allo studio della geometria non euclidea dal punto di vista della geometria differenziale dovrebbe realizzarli concretamente. Tutte le nozioni e i concetti che interverranno in questa breve relazione sono ampiamente illustrati, a un livello elementare, nell'ipertesto La geometria sulla sfera.
Ritagliate una strisciolina rettilinea di cartoncino flessibile (lunga e stretta, ad esempio di 0.5 cm x 30 cm) e applicatela su un pallone o su una palla di polistirolo come vedete nella fotografia seguente.

Non è difficile convincersi che la strisciolina aderisce alla palla lungo archi geodetici. Nella fotografia precedente vedete ad esempio l'arco geodetico AB; come sappiamo si tratta di un arco di circonferenza massima e, trattandosi in questo caso di un arco minore, rappresenta il percorso più breve, sulla superficie sferica, tra i punti A e B. E' importante capire che non è possibile far aderire la nostra strisciolina lungo percorsi che non siano archi geodetici, ad esempio lungo circonferenze minori (vedi figura seguente). Provate a farlo, vi renderete conto che è impossibile.

Applicando striscioline su un pallone è molto facile costruire dei triangoli sferici, avendo la certezza che i lati siano archi geodetici.

Nella fotografia seguente vediamo una linea geodetica per i punti A e B sulla superficie di un cilindro.

Per gli stessi punti A e B del cilindro passono naturalmente altre geodetiche (ne passano infinite); ne vedete un'altra nella fotografia seguente. Ricorderete infatti che mentre per due punti (non antipodali) della superficie sferica passa una e una sola geodetica (circonferenza massima) ciò non avviene nel caso della superficie cilindrica.

Nelle fotografie seguenti vedete due archi geodetici tra gli stessi punti A e B della superficie di un toro: il primo, rappresentato dalla strisciolina gialla, si avvolge attorno al toro e non è il percorso più breve tra i punti A e B; il secondo, rappresentato dalla strisciolina bianca, non si avvolge attorno al toro ed è il percorso più breve tra i due punti.


Enunceremo ora, in forma intuitiva, un importante teorema sulle geodetiche che conferma quanto osservato negli esperimenti precedenti. La superficie Σ di cui si parla è una superficie sufficientemente regolare come tutte quelle esaminate (e come molte altre che ci troviamo intorno). Per avere un'idea di questa regolarità potete pensare a una superfice senza bordi o fori, tale che "zoomando" in ogni suo punto diventi indistinguibile, in un intorno del punto, da un piano (il piano tangente alla superficie). Tenete presente che il foro centrale del toro della fotografia precedente non è un foro della superficie; da un punto di vista intrinseco la superficie del toro non ha alcun foro, è solo nello spazio tridimensionale che possiamo considerare il toro come un oggetto con un foro centrale.
Ecco il teorema:
Se una strisciolina rettangolare di cartoncino (lunga e stretta) viene applicata su una superficie Σ in modo da essere tangente alla superficie lungo la sua linea mediana allora tale linea mediana si dispone su una geodetica della superficie.

Abbiamo dunque un metodo pratico per determinare le geodetiche di qualsiasi superficie regolare. Ci siamo resi conto, con gli esperimenti precedenti, che il percorso minimo tra due punti A e B è sempre un arco geodetico mentre non è in generale vero che, viceversa, un arco geodetico che congiunga A con B sia il percorso minimo tra A e B (riflettete sulla situazione del cilindro o del toro che abbiamo esaminato nelle fotografie precedenti). Se però i punti A e B si trovano in una regione R sufficientemente piccola di Σ allora esiste uno e un solo arco geodetico che congiunga A con B e che sia interamente contenuto nella regione R; tale arco è il percorso minimo da A a B. Riflettete su queste affermazioni alla luce dei vostri esperimenti.
Curvatura
Realizzeremo ora alcuni esperimenti che ci consentono di capire se una regione di una superficie ha curvatura positiva, negativa o nulla. Tale distinzione è fondamentale perchè la geometria di questa regione sarà ellittica, iperbolica o euclidea in relazione al tipo di curvatura (ellittica se la curvatura è positiva, iperbolica se la curvatura è negativa, euclidea se la curvatura è nulla). L'idea è quella di "schiacciare" la superfice sul piano. Quando cerchiamo di "appiattire" una superficie curva si danno tre possibilità:
Riusciamo ad appiattire la superfice, senza operare lacerazioni o sovrapposizioni. Diremo in questo caso che la superfice ha curvatura nulla (cioè in tutti punti della superficie la curvatura è nulla). Ad esempio qualsiasi regione di superfice cilindrica può essere resa perfettamente piatta ed ha quindi curvatura zero. Riflettete sul fatto che una superfice cilindrica può ottenersi arrotolando un foglio di carta. Può dispiacere ma le cose stanno proprio così: esistono delle superfici che siamo abituati a considerare curve ma che, tecnicamente, vanno considerate prive di curvatura.
Non riusciano ad appiattire la superfice, perchè dovremmo operare delle lacerazioni. E' quello che accade, ad esempio, con una regione di superficie sferica; possiamo pensare, affidandoci all'intuizione, che in questo caso ci sia "meno superficie" di quanto ne serva per essere appiattita. In questo caso diremo che la superficie ha curvatura positiva.
Nella fotografia seguente vedete un pallone che è stato tagliato a metà, lungo una circonferenza massima. Provate ad appiattirlo: non ci riuscirete.

L'unico modo è quello di operare dei tagli radiali come vedete nella fotografia seguente (maggiore è il numero dei tagli, maggiore sarà l'aderenza al piano).

Come vedete tra un taglio e l'altro della superficie si vengono a creare degli spazi che corrispondono a superficie mancante. Se non siete convinti potete tentare un'altro esperimento: prendete un'arancia, tagliatela a metà e svuotatela completamente senza danneggiare la buccia esterna. Ora schiacciate l'involucro dell'arancia esercitando una pressione uniforme con un oggetto piatto, ad esempio con un libro. Vi accorgerete che si creano delle lacerazioni, delle fessure.
Non riusciano ad appiattire la superfice, perchè dovremmo operare delle sovrapposizioni. E' quello che accade, ad esempio, con una regione di superficie a forma di sella; possiamo pensare, affidandoci di nuovo all'intuizione, che in questo caso ci sia "più superficie" di quanta possa stare nel piano. In questo caso diremo che la superficie ha curvatura negativa.
Nella fotografia seguente vedete una superficie a sella.

Potete ottenerla facilmente procedendo in questo modo. Disegnate su un foglio di carta un cerchio e un settore circolare con lo stesso raggio del cerchio e un'ampiezza, diciamo, di 60 gradi (vedi figura seguente). Ritagliate il cerchio e il settore. Tagliate il cerchio lungo un suo raggio in modo che presenti una fessura. Inserite nella fessura il settore e fissatelo ai bordi della fessura con del nastro adesivo trasparente. Naturalmente questa operazione di inserimento non è possibile se si rimane nel piano (stiamo pretendendo di inserire altri 60 gradi in un angolo giro); ma potremo farlo se lascieremo flettere la superficie nella terza dimensione. Otterrete così una superficie a sella (è opportuno applicare del nastro anche sull'altra faccia della superficie). La realizzazione di questo modello è molto istruttiva: vi siete resi conto che una sella invade "più superficie" di quanta possa stare nel piano.

Ora provate ad appiattire la vostra sella sul piano, ad esempio appoggiandoci sopra un libro: vi renderete conto che si formano delle pieghe, delle sovrapposizioni, come vedete nella fotografia seguente.

Le considerazioni precedenti concernono la curvatura di un'intera regione di una superficie o di un'intera superficie: ad esempio la superficie di un pallone ha curvatura positiva in ogni suo punto (inoltre la curvatura è costante, uguale in tutti i punti). Ma esistono superfici che hanno regioni a curvatura positiva e regioni a curvatura negativa come ad esempio la superficie di un toro. Per renderci conto se la curvatura di una superficie è in un punto P positiva o negativa dobbiamo considerare le sezioni normali per P (cioè le curve che si ottengono come sezioni della superficie con un piano passante per la perpendicolare alla superficie in P): se la curvatura in P è positiva tutte le sezioni normali per P volgono la concavità dalla stessa parte rispetto alla normale (comunque orientata), se la curvatura è negativa volgono la concavità sia da una parte che dall'altra. Nella fotografia seguente vedete due sezioni normali per un punto P di una sella: le due curve hanno concavità opposta e ciò ci conferma che la curvatura in P è negativa.

Qui di seguito vedete una superficie a sella di equazione z=x2-y2 generata con Mathematica.

Considerate la superficie della bottiglia in figura (gli spilli rappresentano i vettori normali alla superficie in P e Q). La curvatura nel punto P è positiva o negativa? E nel punto Q?

Somma degli angoli di un triangolo
Nella fotografia seguente vedete un triangolo tracciato su una sella (curvatura negativa). I lati del triangolo sono naturalmente archi geodetici, ottenuti incollando sulla superficie le solite striscioline (e rappresentano i percorsi più brevi per collegare i tre vertici). Sul piano concettuale è importante capire che siamo di fronte proprio a un triangolo: i suoi lati, infatti, sono intrinsecamente rettilinei. Un essere bidimensionale il cui spazio (bidimensionale) fosse questa superficie considererebbe "dritti" i tre lati del triangolo (la curvatura è apprezzabile solo nella terza dimensione). Ora attenzione: se misuriamo i tre angoli del triangolo ci accorgiamo che la loro somma è minore di 180°; nel nostro caso la loro somma è di circa 121° (potete misurare gli angoli con un normale goniometro).

Osservate che nella sella c'è questa volta un foro centrale che ha l'unico scopo di facilitarne la costruzione (qui il settore inserito è stato incollato).
Un esperimento analogo possiamo farlo costruendo dei triangoli sulla superficie di un pallone (curvatura positiva); anche in questo caso incolleremo delle striscioline di cartoncino (usando della colla a presa rapida, tipo Attack, o degli spilli). Potremo verificare che qui la somma degli angoli di un triangolo è sempre maggiore di 180°. Nella fotografia seguente vedete un triangolo sferico la cui somma angolare è di circa 242°.

La questione delle somme angolari è di enorme rilevanza: ricordate infatti che la proprietà dei triangoli (euclidei) di avere la somma degli angoli uguale a un angolo piatto è logicamente equivalente al quinto postulato. Osservando le fotografie seguenti che mostrano una superficie a sella da due diversi punti di vista, potete rendervi conto che per un punto P esterno ad una retta r (cioè ad una geodetica r) passano infinite parallele ad r (cioè infinite rette che non intersecano r); in particolare ne vedete due: le rette s e t (ma anche tutte quelle "comprese" tra s e t non intersecano r).

Congruenza di figure e sovrapponibilità
Per il prossimo esperimento dovete utilizzare due palloni identici ed essere disposti a sacrificare uno dei due. Da uno dei due palloni ritagliate una figura qualsiasi, ad esempio un triangolo; poi disponete il triangolo sul secondo pallone come vedete nella fotografia seguente.

Vi renderete facilmente conto di poter muovere liberamente il triangolo sulla superficie del pallone, in ogni direzione, senza alterarne lunghezza dei lati e ampiezza degli angoli, e mantenendolo aderente alla superficie. Accade in sostanza ciò che accade nel piano euclideo dove possiamo muovere isometricamente una figura (mediante traslazioni e rotazioni) senza mai uscire dal piano stesso. Questa proprietà della sfera è di fondamentale importanza nella costruzione di una geometria perchè potremo parlare di congruenza (diretta) di figure come sovrapponibilità. Due figure sulla sfera sono direttamente congruenti se possiamo sovrapporle con una rotazione in sé della sfera.
Una cosa simile non accade su ogni superficie. Realizzate l'esperimento seguente. Procuratevi una superficie rigida a forma di ciambella e ritagliatene un tassello come vedete nella fotografia seguente.

Provate a muovere il tassello rimanendo in una regione ove la superficie ha la stessa curvatura del tassello: riuscirete a mantenerlo aderente alla superficie stessa (vedi fotografia seguente).

Cercate ora di portare il tassello verso l'interno della superficie facendolo scorrere sulla superficie: vi renderete conto che l'operazione non è possibile se pretendiamo che il tassello rimanga aderente alla superficie stessa (vedi fotografia seguente).

Il problema consiste nel fatto che la nostra superficie non ha curvatura costante (cioè la curvatura cambia da punto a punto: sappiamo ad esempio che in alcuni punti è positiva e in altri negativa). Il grande matematico tedesco Carl Friedrich Gauss (1777-1855), il primo ad occuparsi della geometria su una superficie, ha dimostrato che se vogliamo far "scorrere" una figura su una superficie in modo che, al più, la figura si fletta ma non si deformi (cioè rimanga invariata la sua metrica, si conservino angoli e distanze tra punti) allora la superficie deve avere curvatura costante (positiva o negativa). Ciò accade ad esempio sulla sfera che ha curvatura positiva costante (o sul piano euclideo che ha curvatura costantemente nulla).
Il matematico italiano Eugenio Beltrami (1835-1900) ha dimostrato che esistono anche delle superfici a curvatura costante negativa (superfici pseudosferiche); tali superfici, ammettendo dei movimenti in sé con flessione ma senza estensione del tutto analoghi a quelli del piano e della sfera, consentono di parlare di congruenza di figure come sovrapponibilità. Su una superficie pseudosferica la somma degli angoli di un triangolo è naturalmente minore di 180°. Nella figura seguente vedete una superficie pseudosferica, generata con Mathematica, di equazioni parametrichex(u,v) = cos(u) sin(v)
y(u,v) = sin(u) sin(v)
z(u,v) = cos(v) + log(tan(v/2))
0 ≤ u ≤ 2π
0 < v < πSi osservi che al variare di v nell'intervallo (0, π) il valore di z varia da -∞ a +∞; nella superficie qui di seguito l'intervallo di variazione per v è h < v < π - h con h=0.1. Il valore di h determina di quanto la pseudosfera verrà troncata superiormente e inferiormente.

Congruenza inversa sulla superficie sferica
Nella figura seguente vedete due triangoli sferici simmetrici rispetto al centro della sfera. I due triangoli hanno angoli e lati corrispondenti uguali e sono da considerarsi uguali, pur non essendo sovrapponibili con una rotazione della sfera in sé. Diremo che i due triangoli sono inversamente congruenti. Una cosa analoga accade nel piano dove abbiamo figure direttamente e inversamente congruenti, ad esempio due triangoli scaleni simmetrici rispetto a una retta sono inversamente congruenti (hanno lati e angoli corrispondenti uguali ma non sono sovrapponibili se si rimane nel piano).
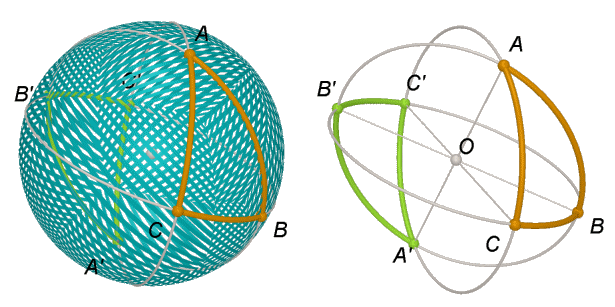
Per un'immagine dinamica di triangoli sferici antipodali, realizzata con GeoGebra, vedi anche triangoli sferici.

