Indice    Paragrafo precedente    Paragrafo successivo   

Siamo ora pronti per dimostrare il teorema fondamentale sui triangoli sferici. Assumeremo come sempre una sfera unitaria e misureremo gli angoli in radianti.

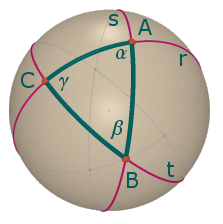Nella figura a fianco vedete il triangolo sferico ABC; consideriamo la somma S degli angoli

S = α + β + γ

Ci siamo resi conto, nel paragrafo 17, che S non è costante ma varia al variare del triangolo. Il nostro obiettivo è quello di esprimere S in funzione di un unico parametro che rappresenti una grandezza associabile ad ogni dato triangolo. La congettura formulata nel paragrafo 17 suggerisce che questo parametro sia proprio l'area del triangolo. Proviamolo.

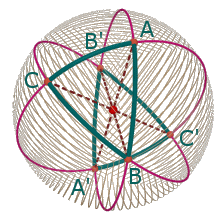Osserviamo in primo luogo che al triangolo ABC corrisponde un triangolo antipodale A'B'C' uguale ad ABC (vedi figura a sinistra). I triangoli ABC e A'B'C' sono, per la precisione, inversamente uguali (o inversamente congruenti) in quanto simmetrici rispetto al centro della sfera; i due triangoli hanno lati e angoli corrispondenti uguali (congruenti) ma non sono, in generale, sovrapponibili con un movimento rigido, cioè facendo "scorrere" ABC sulla superficie sferica fino a portarlo sopra A'B'C'. A noi tuttavia interessa che i due triangoli abbiano la stessa area ed è questo che dovete tener presente.

Triangoli antipodali

Triangoli antipodali (sfera invisibile)

Consideriamo ora i tre doppi fusi della figura seguente: il primo è individuato dalle circonferenze massime r ed s, il secondo da s e t, il terzo da r e t. Gli angoli dei fusi sono gli angoli del nostro triangolo cioè sono rispettivamente α, β, γ.

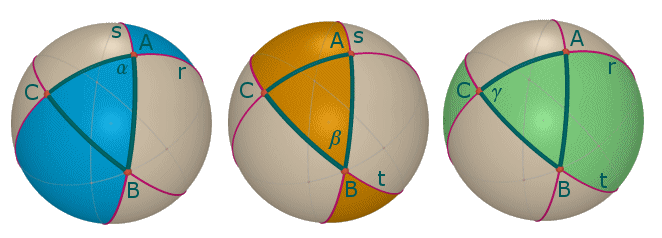
Se consideriamo contemporaneamente i tre doppi fusi ci accorgiamo che ricoprono tutta la superficie sferica; inoltre i due triangoli ABC e A'B'C' vengono ricoperti tre volte; potete infatti notare che il triangolo ABC viene ricoperto successivamente in azzurro, arancione e verde e lo stesso accade per il triangolo antipodale. Allora possiamo scrivere

area sup. sferica =
     area dei tre doppi fusi
     - 2 volte area triangolo ABC
     - 2 volte area triangolo A'B'C'

Quindi, tenendo conto che i due triangoli ABC e A'B'C' hanno la stessa area e applicando la formula che fornisce l'area di un doppio fuso, si ha

4π = 4α+4β+4γ-4A

dove abbiamo indicato con A l'area del nostro triangolo ABC. Ne segue la formula

α+β+γ = π+A

Si ha dunque il seguente fondamentale teorema

Teorema Assumendo una sfera unitaria e la misura degli angoli in radianti, la somma degli angoli di un triangolo sferico è sempre maggiore di un angolo piatto ed è uguale a un angolo piatto più l'area del triangolo.

Somma degli angoli di un triangolo sferico

La formula precedente si può leggere anche così

Corollario Assumendo una sfera unitaria, l'area di un triangolo sferico è uguale alla somma dei suoi angoli (misurati in radianti) meno π.

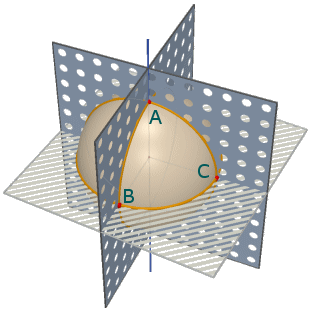Verifichiamo la nostra formula nel caso del triangolo trirettangolo ABC della figura a fianco; tale triangolo ha evidentemente area uguale a 1/8 dell'area della sfera cioè ha area π/2. Applicando la formula si ha

A = α + β + γ - π =

= π/2 + π/2 + π/2 - π =

= π/2