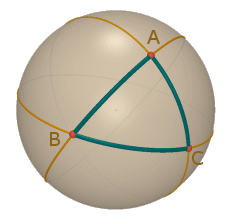Nella figura a fianco vedete un triangolo sferico: i suoi tre lati sono naturalmente segmenti di S², cioè archi geodetici. Da un punto di vista intrinseco dovremmo parlare semplicemente di triangolo. Cerchiamo di definire più precisamente un triangolo sferico. Nel piano euclideo tre punti non allineati individuano uno e un sol triangolo: basta collegare coppie di punti con un segmento.



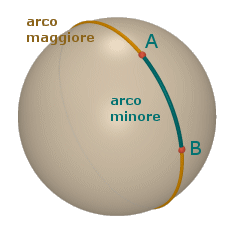
Le cose si complicano su S². In primo luogo due punti non antipodali possono essere collegati con due diversi segmenti (un arco minore e un arco maggiore di circonferenza massima, come si vede nella figura a sinistra). Stabiliamo allora di considerare solo archi minori.

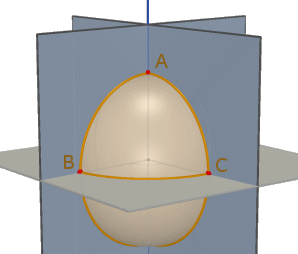
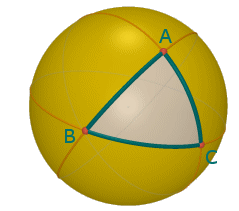C'è poi da osservare che tre archi minori, non disposti (a due a due) sulla stessa circonferenza massima e aventi a coppie un estremo in comune, delimitano due regioni sulla sfera. Chiamiamo allora triangolo sferico quella regione, delle due, che ha area minore. In tal modo tre archi minori individuano un'unica regione triangolare che ha sempre area minore della superficie di una semisfera. Nella figura a fianco vedete rispettivamente in grigio e in giallo le due regioni delimitate da tre archi minori: il triangolo sferico ABC è allora quello grigio.

Triangoli sferici

Triangoli sferici (circonferenze massime visibili)


Ora osserviamo la figura a sinistra. Ogni lato del triangolo ABC è lungo 1/4 di circonferenza massima cioè π/2 e l'area del triangolo è pari a 1/8 dell'area di S² cioè è uguale, ancora, a π/2 (non dimenticate che abbiamo assunto una sfera di raggio unitario che ha area 4π). Ma la cosa più importante da osservare è la somma degli angoli: nel nostro caso è di 270°. Viene dunque a cadere il teorema euclideo sulla somma degli angoli di un triangolo. Ma c'è di più: mentre la somma degli angoli è costante per i triangoli euclidei, per i triangoli sferici tale somma varia al variare del triangolo. Ce ne rendiamo conto osservando la figura seguente.

Triangoli sferici birettangoli

Triangoli sferici birettangoli (piani visibili)

Triangoli sferici birettangoli (animazione)

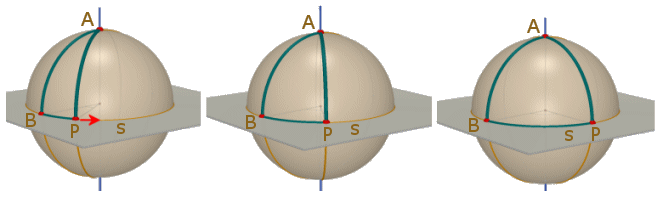
Come vedete A è un polo per la retta s e i segmenti AB e AP sono perpendicolari a s. I triangoli APB che vengono a formarsi al variare di P su s hanno, tutti, due angoli retti mentre il terzo angolo, quello in A, varia. E' quindi variabile anche la somma degli angoli. Per tutti questi triangoli la somma degli angoli è maggiore di 180° e si capisce che facendo tendere a zero l'angolo in A la somma degli angoli tende a 180°. Si direbbe che la somma degli angoli vari al variare dell'area del triangolo: tanto maggiore è l'area tanto maggiore è la somma angolare, tanto più l'area si avvicina a zero tanto più la somma angolare si avvicina a 180°. Riflettete anche sulla seconda domanda che si trova alla fine del paragrafo. Formuliamo la seguente congettura

Congettura La somma degli angoli di un triangolo sferico varia al variare della sua area.

Non deve sorprenderci il fatto che per i triangoli sferici non valga la proprietà euclidea della somma degli angoli di un triangolo. Come si è già detto (vedi paragrafo 5) tale proprietà discende dall'esistenza di rette parallele e dal quinto postulato di Euclide e, come sappiamo, nella geometria di S² non sussistono tali presupposti mentre vale l'assioma ellittico.

Domanda Nel piano euclideo tre rette non passanti per uno stesso punto e tali da intersecarsi a due a due, individuano uno e un solo triangolo. Cosa si può dire per tre rette di S²?

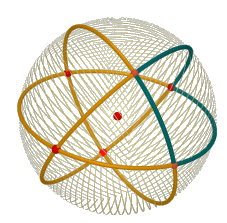
[Soluzione. Tre rette di S² non passanti per uno stesso punto individuano otto triangoli sferici (a due a due antipodali). Nella figura a destra è stato evidenziato in verde uno degli otto triangoli.]

Domanda Sapete dire qual è l'estremo superiore per la somma degli angoli di un triangolo sferico ?

[Soluzione. Data la nostra definizione di triangolo sferico, la somma degli angoli è sempre minore di 540° poiché ogni angolo è minore di 180°; fate qualche esperimento con le figure dinamiche di GeoGebra: se un angolo diventa di 180° i tre vertici del triangolo si trovano su una stessa circonferenza massima e dobbiamo escluderlo. D'altra parte ciascuno dei tre angoli può avvicinarsi quanto vogliamo a 180° (vedi figura a fianco). Quando ognuno dei tre angoli tende a 180°, l'area del triangolo tende all'area della semisfera che rappresenta l'estremo superiore per le aree dei triangoli sferici.]