Indice    Paragrafo precedente    Paragrafo successivo   

Riprendiamo il filo del discorso iniziato nel paragrafo 13: abbiamo detto che le circonferenze massime di S², cioè le geodetiche, non hanno curvatura intrinseca. Ma se assumiamo il punto di vista estrinseco, cosa si può dire?

Consideriamo due punti non antipodali A e B sulla superficie sferica e la retta AB che attraversa la sfera nello spazio tridimensionale. Consideriamo il fascio di piani per A e B (li ottenete facendo ruotare il piano α della figura seguente attorno all'asse AB). Ognuno di questi piani stacca sulla superficie sferica una circonferenza per A e B. Tra queste circonferenze avremo una (e una sola) circonferenza massima quando il piano α passa per il centro O della sfera.

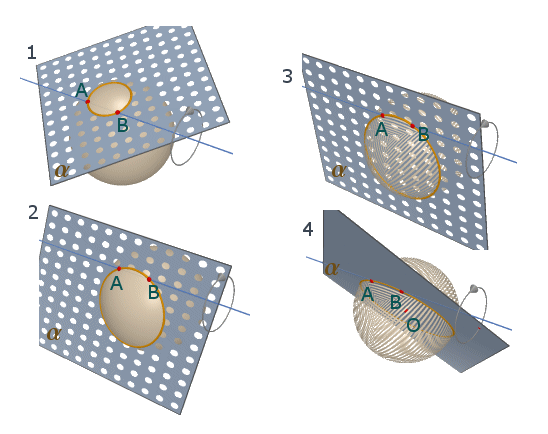
Circonferenze per due punti

Circonferenze per due punti (animazione)

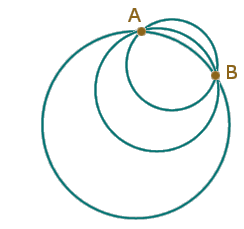Ora supponiamo di rappresentare tutte queste circonferenze in uno stesso piano, come in figura a fianco. Si capisce che il percorso minimo tra A e B sarà l'arco di minor curvatura cioè l'arco della circonferenza massima (come del resto ci aspettavamo). La circonferenza massima è quella di raggio r, dove r è il raggio della sfera. Questa circonferenza che in S² non ha curvatura (è una geodetica, è una retta, se pensate all'esperimento del carrellino la ruota di sinistra percorre lo stesso spazio di quella di destra), ha invece curvatura 1/r quando viene rappresentata nel piano. Si tratta, ripetiamolo, di curvatura estrinseca. Possiamo quindi concludere che: le geodetiche di S² sono le circonferenze che hanno curvatura estrinseca minima.

Le questioni a cui abbiamo accennato invitano alla riflessione. Quello che segue è un dialogo immaginario tra una creatura bidimensionale, una tartaruga 2D, e un osservatore esterno, tridimensionale, che chiameremo Achille. La tartaruga è confinata sulla superficie di una sfera mentre Achille è in grado di osservare il mondo della tartaruga immerso nello spazio 3D. Il dialogo illustra due punti di vista radicalmente diversi: quello intrinseco della tartaruga e quello estrinseco di Achille.

Tartaruga E' successo qualcosa di veramente strano: sono partita dal punto A, dove ho piantato una bandierina, sono poi andata sempre in direzione nord, senza mai ruotare, ma sono tornata, dopo un lungo percorso, al punto di partenza. Una forza misteriosa deve avermi fatto ruotare senza che io potessi accorgermene, devi avermi costretto a percorrere una circonferenza anziché una retta. Oppure qualche diabolico essere ha spostato la bandierina senza che io me ne accorgessi.

Achille Le cose non stanno così: in realtà non sei andata dritto ma ti sei mossa lunga una linea curva, ecco perché sei tornata al punto di partenza. Non c'è alcuna forza misteriosa né alcun demone che abbia spostato la bandierina.

Tartaruga Ma via! Saprò bene quando vado dritto o quando sto curvando. Guarda, ecco un esperimento inconfutabile: pianto due paletti ad una certa distanza e tendo tra di loro un filo. Se cammino lungo il filo sto certamente andando dritto; utilizzando questo espediente ho imparato a camminare lungo percorsi perfettamente rettilinei.

Achille In un certo senso sei effettivamente andata dritto, ma è lo spazio che ti ha costretto a curvare; il tuo spazio, bidimensionale, è infatti uno spazio curvo: si chiama spazio sferico o superficie sferica. Tu non puoi rendertene conto ma quando metti in tensione il filo tra due punti ottieni in realtà un arco di curva. Linee che a te appaiono rette sono in realtà linee curve: ma la curvatura è nella terza dimensione e tu non puoi apprezzarla. Anche un raggio luminoso si muove lungo un arco di curva. Per calcolare il tuo cambiamento di direzione lungo un percorso devi tener conto sia delle rotazioni da te effettuate sia della curvatura dello spazio. Quella che tu chiami forza misteriosa è in realtà una proprietà geometrica dello spazio.

Tartaruga Sembra incredibile ma vediamo se ho capito. Tu sostieni che durante qualsiasi cammino devo tener conto di due tipi di rotazioni: le rotazioni che io decido di fare e la rotazione che lo spazio, tu lo chiami spazio "sferico", mi costringe ad effettuare senza che io me ne accorga?

Achille Proprio così.