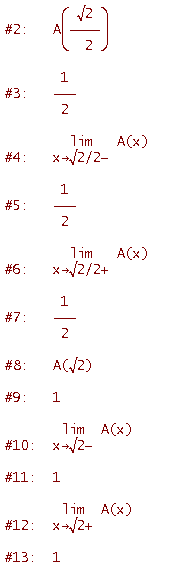Attività successiva
Attività precedente
Home
Per tracciare funzioni definite a tratti nel modo più semplice usa EffeDiX (free)

Funzioni definite a tratti
La condizione cond potrebbe essere, ad esempio,
Ecco il codice di Derive
Come vedi, si tratta del grafico di una parabola per x minore o uguale a 1 e di una retta per x maggiore di 1. I due tratti sono, come sai, funzioni continue e anche il raccordo tra i due tratti è continuo, non ci sono salti. Verifichiamo analiticamente che nel punto di raccordo x=1 la funzione è continua
Abbiamo la verifica della continuità: il limite di f(x) per x che tende a 1 da sinistra è uguale al limite per x che tende a 1 da destra e tali limiti sono uguali a f(1). Per avere un'idea intuitiva della continuità (e un supporto visivo!) fai così:
inserisci nella finestra grafica una slider bar per la variabile t con t che varia, diciamo, da -4 a 4;
trascinando il cursore della slider bar vedrai che il punto [t, f(t)] si muove con continuità sul grafico, senza salti o interruzioni.
Ecco il codice di Derive
Fai attenzione, qui ci sono due comandi IF nidificati uno nell'altro. La struttura è questa:
Ciascuno dei tre tratti è una funzione continua; non rimane quindi che studiare la continuità nei punti di raccordo. Nel primo punto di raccordo, in x=2, si ha
Quindi la funzione non è continua in x=2 (il limite sinistro è diverso dal limite destro). Nel secondo punto di raccordo, in x=5, si ha
Se fai muovere un punto [t, f(t)] sul grafico, mediante una slider bar, come si è detto nell'esperimento precedente, noterai che fa un salto in x=2.
Occupiamoci ora della derivabilità. Ogni tratto è costituito da funzioni derivabili: dobbiamo esaminare i punti di raccordo. In x=2, la funzione non è continua e quindi non è derivabile. Studiamo la situazione in x=5 in cui la funzione è continua e quindi potrebbe essere derivabile
Quindi la funzione non è derivabile in x=5 (infatti non esiste il limite del rapporto incrementale: il limite sinistro è diverso dal limite destro).
Nota che per x=2 e per x=5 alla funzione g(x) viene assegnato il valore "?"; ciò indica che g(x) non è definita per x=2 e x=5 ovvero che f(x) non è derivabile in x=2 e x=5. Scriviamo le coordinate di un generico punto [t, f(t)] del grafico di f(x) e l'equazione della tangente al grafico in tal punto
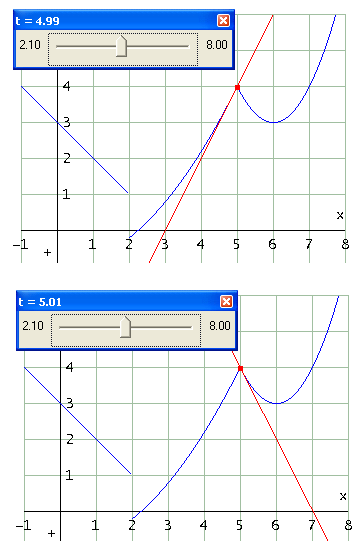
Non rimane che inserire nella finestra grafica una slider bar per la variabile t, ad esempio per t che varia da 2,1 a 8; poi tracceremo il grafico relativo alle righe #20 e #21. Trascinando il cursore vedremo la tangente muoversi con continuità sul grafico ma, attento, per t=5 noteremo un brusco cambiamento di direzione della tangente: in quel punto f(x) non è derivabile, il grafico non è liscio, c'è un punto angoloso. Nella figura seguente vedi la tangente per t di poco minore di 5 e per t di poco maggiore di 5.
Osservazione Non c'è limite al numero di comandi IF che puoi nidificare uno nell'altro; in tal modo puoi definire una funzione qualunque sia il numero dei tratti. Tieni presente però che la sintassi diventa via via più complessa (con un numero di parentesi che via via aumenta) perciò è opportuno, prima di implementare la funzione, tracciare un diagramma ad albero come quello dell'esempio 2. Inoltre puoi utilizzare nella definizione di una funzione a tratti altre funzioni a tratti (già definite).
Nella seguente figura dinamica di Cabri, la regione comune ai due quadrati è quella arancione. Tascinando il punto indicato vedi come varia la regione; si intuisce che la sua area è una funzione definita a tratti del lato EF.
Verifichiamo analiticamente che A(x) è continua nei punti di raccordo
 Il comando che useremo per definire una funzione a tratti con Derive è il comando IF (se). Eccone la sintassi più utilizzata
Il comando che useremo per definire una funzione a tratti con Derive è il comando IF (se). Eccone la sintassi più utilizzata
IF(cond, espr1, espr2)
che puoi interpretare così
SE è verificata la condizione cond
ALLORA il comando fornisce in uscita l'espressione espr1
ALTRIMENTI fornisce l'espressione espr2
x > 3
oppure
x > 3 and x<=5
Facciamo qualche esperimento.

Esperimento 1
Definiamo la funzione a tratti
e studiamone la continuità.
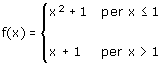


ed ecco come devi digitare il comando nel campo di input
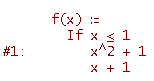
Facciamo qualche verifica

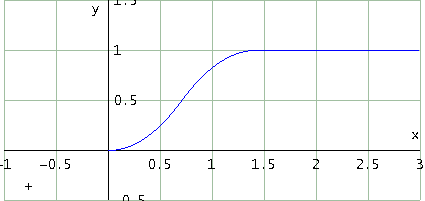
Sì, funziona. Tracciamo il grafico (selezionando, ovviamente, la riga #1)


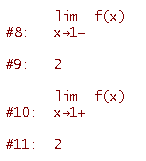

Esperimento 2
Definiamo la funzione a tratti
e studiamone continuità e derivabilità.
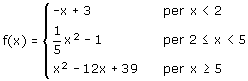

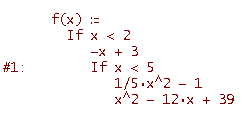
Ecco il grafico
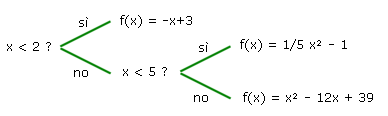

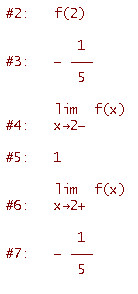
Quindi la funzione è continua in x=5.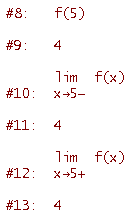

Ora, per avere un'idea intuitiva della derivabilità, vogliamo tracciare la tangente al grafico di f(x) (vogliamo una tangente dinamica, pilotata attraverso una slider bar). Prima di tutto definiamo la funzione derivata g(x) di f(x) che sarà naturalmente una funzione definita a tratti
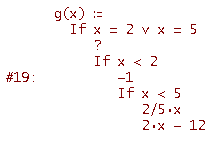


Esperimento 3
Un quadrato ABCD ha lato unitario e un secondo quadrato EFGH ha i vertici sugli assi di simmetria del primo quadrato. Determiniamo l'area della regione di piano comune ai due quadrati al variare della misura del lato EF del secondo quadrato (da 0 a +inf).


Indichiamo con A(x) l'area della regione in funzione del lato x. Ragionando sulle figure a fianco ti rendi conto che si ha:

L'intuizione geometrica (vedi figura dinamica) suggerisce che A(x) sia una funzione continua in tutto il suo dominio; definiamo la funzione con Derive. Ecco il diagramma ad albero che ci aiuta a scrivere il codice di Derive
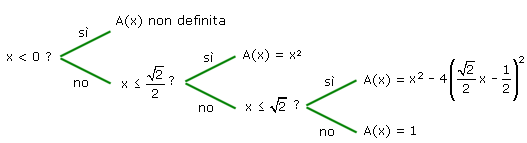
Ed ecco il codice, avendo semplificato l'espressione nell'ultimo ramo "sì"
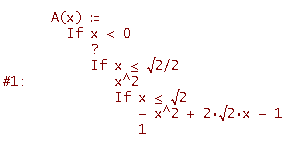
E questo è il grafico