Indice    Paragrafo precedente   

Nel paragrafo precedente abbiamo visto che la superficie di un toro non è uno spazio omogeneo, la curvatura varia da punto a punto, assumendo valori positivi, nulli, negativi; come conseguenza si ha che la geometria nelle varie ragioni cambierà in relazione al tipo di curvatura. Vogliamo fare qualche esperimento per convincerci che le cose stanno proprio così. Non opereremo però sulla superficie di un toro ma sulla superficie del solido cavo a facce piane della figura a fianco che è topologicamente equivalente ad un toro e che mostra, come vedremo, una qualche analogia con la curvatura del toro.

Per discriminare il tipo di geometria ricorreremo alla studio delle somme angolari per un poligono tracciato sulla superficie. Ricordiamo, a questo proposito, che nel piano euclideo la somma s degli angoli, misurati in radianti, di un poligono con n lati è data da

s = (n-2)π

s > (n-2)π

s < (n-2)π

E' chiaro che l'uguaglianza e le due disuguaglianze precedenti discendono tutte dal fatto che la somma degli angoli di un triangolo è, nel caso ellittico, maggiore di π, nel caso euclideo uguale a π, nel caso iperbolico minore di π. Un poligono su una superficie è naturalmente limitato da archi geodetici (così come nel piano euclideo è limitato da segmenti).

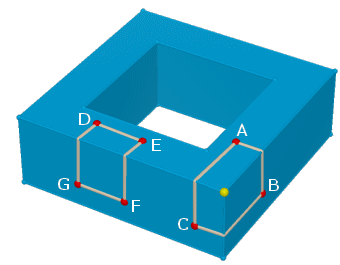Bene, possiamo iniziare i nostri esperimenti. Sul solido è stato tracciato un triangolo ABC (vedi figura a fianco). Attenzione, dovete essere convinti che si tratta di un triangolo intrinseco; i tre lati AB, BC, CA sono archi geodetici (se la cosa non vi convince andate a rivedere il paragrafo 11). Il triangolo, come vedete, ha tre angoli retti. Siamo dunque in una situazione ellittica (s > π). Notate che il triangolo contiene un vertice del solido cavo (il vertice è evidenziato in giallo). Osservate ora il quadrilatero DEFG (è un rettangolo intrinseco): qui la somma s degli angoli è 2π e siamo quindi in una situazione euclidea. Notate che all'interno del rettangolo non ci sono vertici del solido cavo. Potremmo allora ipotizzare che la curvatura del nostro solido si concentri tutta nei vertici (mentre, ripensando al caso del toro, la curvatura varia con continuità su tutta la superficie).

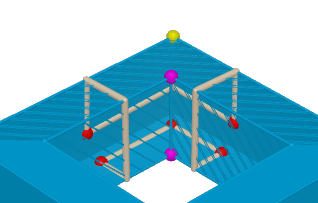
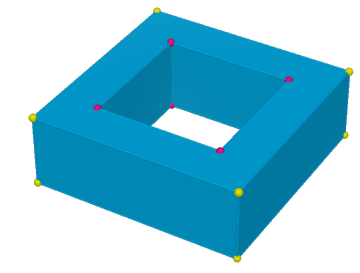I vertici in cui si concentra curvatura positiva dovrebbero essere quelli "esterni" (sono otto, evidenziati in giallo in figura) mentre quelli in cui si concentra curvatura negativa sono "interni" cioè quelli che circondano internamente il foro (sono di nuovo otto, evidenziati in viola in figura). Ci si convince, con qualche esperimento, che le cose stanno proprio così.

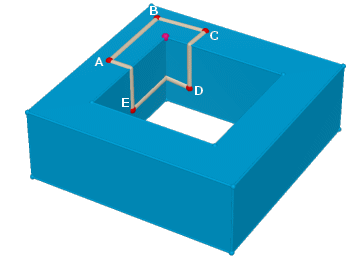Proviamo ad esempio a considerare un poligono sulla superficie che contenga al suo interno un vertice del solido in cui deve concentrarsi curvatura negativa. Osservate il pentagono ABCDE della figura a fianco. La somma degli angoli è pari a cinque angoli retti, cioè s = 5π/2 < 3π. Come ci aspettavamo, siamo in una situazione iperbolica.

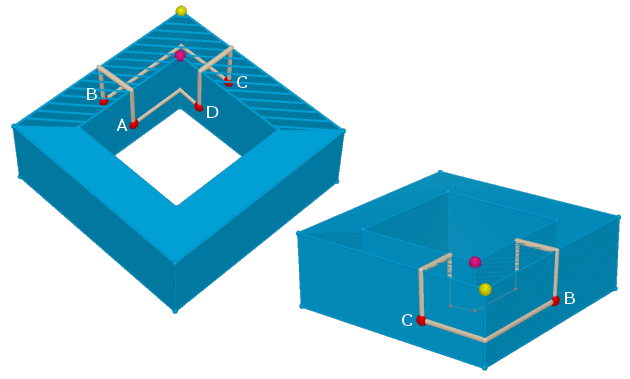
Nella figura seguente abbiamo considerato un rettangolo ABCD che ingloba due vertici del solido cavo: uno (giallo) in cui si concentra curvatura positiva e uno (viola) in cui si concentra curvatura negativa. Possiamo ritenere che i due vertici si compensino l'uno con l'altro in modo che la somma degli angoli sia di tipo euclideo. Ed è proprio così: s = 2π.