Indice Paragrafo precedente Paragrafo successivo

12. Curvatura
 State guidando su una strada in cui si alternano tratti rettilinei e tratti con curve. Vi trovate, in questo momento, su un tratto rettilineo: non avete bisogno di sterzare, non avete bisogno di modificare la traiettoria rettilinea dell'automobile. Diremo che in questo punto del percorso la curvatura è zero. Ora state affrontando una curva "larga": dovete agire sullo sterzo, dovete modificare la traiettoria rettilinea ma lo farete lievemente, con una piccola rotazione dello sterzo. In questo punto il percorso ha una "piccola" curvatura. Ecco infine una curva "stretta": dovete agire sullo sterzo molto rapidamente, ruotandolo più di prima. Potremmo dire che ora vi allontanate dalla traiettoria rettilinea, cioè dalla tangente al percorso, più rapidamente di quanto non abbiate fatto nella curva precedente. In questo punto il percorso ha una "grande" curvatura.
State guidando su una strada in cui si alternano tratti rettilinei e tratti con curve. Vi trovate, in questo momento, su un tratto rettilineo: non avete bisogno di sterzare, non avete bisogno di modificare la traiettoria rettilinea dell'automobile. Diremo che in questo punto del percorso la curvatura è zero. Ora state affrontando una curva "larga": dovete agire sullo sterzo, dovete modificare la traiettoria rettilinea ma lo farete lievemente, con una piccola rotazione dello sterzo. In questo punto il percorso ha una "piccola" curvatura. Ecco infine una curva "stretta": dovete agire sullo sterzo molto rapidamente, ruotandolo più di prima. Potremmo dire che ora vi allontanate dalla traiettoria rettilinea, cioè dalla tangente al percorso, più rapidamente di quanto non abbiate fatto nella curva precedente. In questo punto il percorso ha una "grande" curvatura.
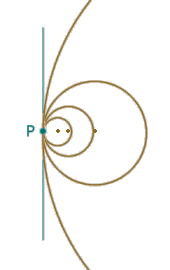 Abbiamo dato un'idea intuitiva di cosa si intenda, nel piano euclideo, per curvatura di una linea in un dato punto. Come possiamo dare significato matematico a questa nozione intuitiva? Cominciamo a ragionare sulle linee piane più semplici che conosciamo. Per le rette c'è poco da dire: non c'è curvatura in alcun punto, la curvatura è sempre nulla. Consideriamo invece delle circonferenze; osserviamo in particolare la figura a fianco in cui vediamo alcune circonferenze, di raggio diverso, passanti tutte per un punto P e con il centro su una stessa retta per P. Cosa possiamo dire della curvatura in P? E' facile capire che se aumenta il raggio delle nostre circonferenze la curvatura diminuisce. E' allora abbastanza naturale definire la curvatura per ciascuna circonferenza come l'inverso del suo raggio r
Abbiamo dato un'idea intuitiva di cosa si intenda, nel piano euclideo, per curvatura di una linea in un dato punto. Come possiamo dare significato matematico a questa nozione intuitiva? Cominciamo a ragionare sulle linee piane più semplici che conosciamo. Per le rette c'è poco da dire: non c'è curvatura in alcun punto, la curvatura è sempre nulla. Consideriamo invece delle circonferenze; osserviamo in particolare la figura a fianco in cui vediamo alcune circonferenze, di raggio diverso, passanti tutte per un punto P e con il centro su una stessa retta per P. Cosa possiamo dire della curvatura in P? E' facile capire che se aumenta il raggio delle nostre circonferenze la curvatura diminuisce. E' allora abbastanza naturale definire la curvatura per ciascuna circonferenza come l'inverso del suo raggio r
curvatura = 1/r
Osservate che questa definizione è indipendente dalla scelta del punto P: per una data circonferenza la curvatura dipende solo dal raggio ed è uguale in tutti i punti. Questo non ci meraviglia data l'assoluta simmetria delle circonferenze (ogni punto è, per i nostri fini, assolutamente equivalente agli altri). Del resto se doveste guidare un'automobile su un percorso perfettamente circolare non dovreste, una volta trovata la giusta rotazione dello sterzo, effettuare più alcuna correzione. Quindi:
Proprietà Le circonferenze sono linee piane a curvatura costante e la loro curvatura è uguale all'inverso del raggio.
Si potrebbe dimostrare che le uniche linee piane a curvatura costante sono le rette (curvatura zero) e le circonferenze (curvatura 1/r).
 Se aumenta il raggio di una circonferenza la sua curvatura (in qualsiasi punto) diminuisce (la curvatura di una circonferenza è l'inverso del raggio)
Se aumenta il raggio di una circonferenza la sua curvatura (in qualsiasi punto) diminuisce (la curvatura di una circonferenza è l'inverso del raggio)
 Vediamo rapidamente come si possa definire la curvatura in un punto P per una generica linea curva γ che si trovi nel piano.
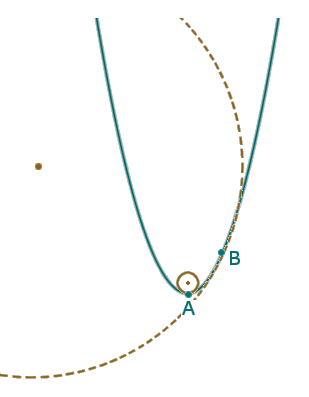
L'idea è questa: cerchiamo di approssimare, nelle vicinanze di P, la nostra linea con una circonferenza; se ci riusciamo il gioco è fatto, diremo che la curvatura di γ in P è uguale alla curvatura di questa circonferenza. Ma come determinare la circonferenza che meglio approssima γ in P? Consideriamo due punti A e B su γ vicini al punto P (vedi figura a fianco). Sappiamo che per tre punti non allineati passa una e una sola circonferenza, quindi per A, P e B passa una ben determinata circonferenza. Ora facciamo tendere verso P sia il punto A che il punto B (facendoli muovere sempre sulla nostra curva γ: si intuisce che individueremo una circonferenza limite. E' questa la circonferenza che cerchiamo: prende il nome di circonferenza osculatrice a γ in P. E' anche chiaro cosa si debba intendere per raggio di curvatura e centro di curvatura per una curva γ in P: si tratta rispettivamente del raggio e del centro della circonferenza osculatrice a γ in P.
Vediamo rapidamente come si possa definire la curvatura in un punto P per una generica linea curva γ che si trovi nel piano.
L'idea è questa: cerchiamo di approssimare, nelle vicinanze di P, la nostra linea con una circonferenza; se ci riusciamo il gioco è fatto, diremo che la curvatura di γ in P è uguale alla curvatura di questa circonferenza. Ma come determinare la circonferenza che meglio approssima γ in P? Consideriamo due punti A e B su γ vicini al punto P (vedi figura a fianco). Sappiamo che per tre punti non allineati passa una e una sola circonferenza, quindi per A, P e B passa una ben determinata circonferenza. Ora facciamo tendere verso P sia il punto A che il punto B (facendoli muovere sempre sulla nostra curva γ: si intuisce che individueremo una circonferenza limite. E' questa la circonferenza che cerchiamo: prende il nome di circonferenza osculatrice a γ in P. E' anche chiaro cosa si debba intendere per raggio di curvatura e centro di curvatura per una curva γ in P: si tratta rispettivamente del raggio e del centro della circonferenza osculatrice a γ in P.
Naturalmente per una generica linea curva piana la curvatura varierà al variare del punto P (al contrario di quanto accade per le circonferenze che hanno curvatura costante). Ad esempio la curvatura in P di una parabola varia con continuità al variare con continuità di P sulla curva. Man mano che P si allontana dal vertice, da una parte o dall'altra, la curvatura tende a zero (vedi la figura seguente).
 Circonferenza osculatrice
Circonferenza osculatrice
Consideriamo ora nel piano due punti A e B e le circonferenze che passano per A e B (sono infinite, hanno tutte il centro sull'asse del segmento AB). Nella figura seguente ne vediamo alcune.
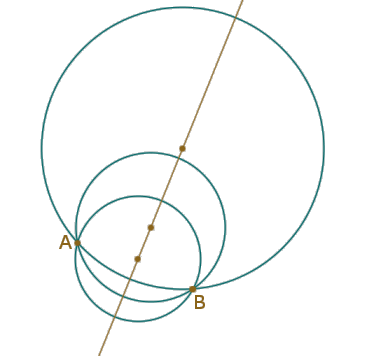
Si capisce che tanto maggiore è il raggio della circonferenza, quindi tanto minore è la curvatura, tanto minore sarà la lunghezza dell'arco AB di circonferenza. Anzi ci rendiamo conto che facendo tendere il raggio all'infinito, e quindi la curvatura a zero, l'arco AB tende al segmento AB.
 Domanda
Dati due punti A e B del piano euclideo, esiste un arco minimo di circonferenza per A e B?
Domanda
Dati due punti A e B del piano euclideo, esiste un arco minimo di circonferenza per A e B?
[Soluzione. No, non esiste. La lunghezza degli archi di circonferenza per A e B ha come estremo inferiore, ma non come minimo, la lunghezza del segmento AB.]